Michael96
Member
I bought tickets for this trip for the April, 1 -
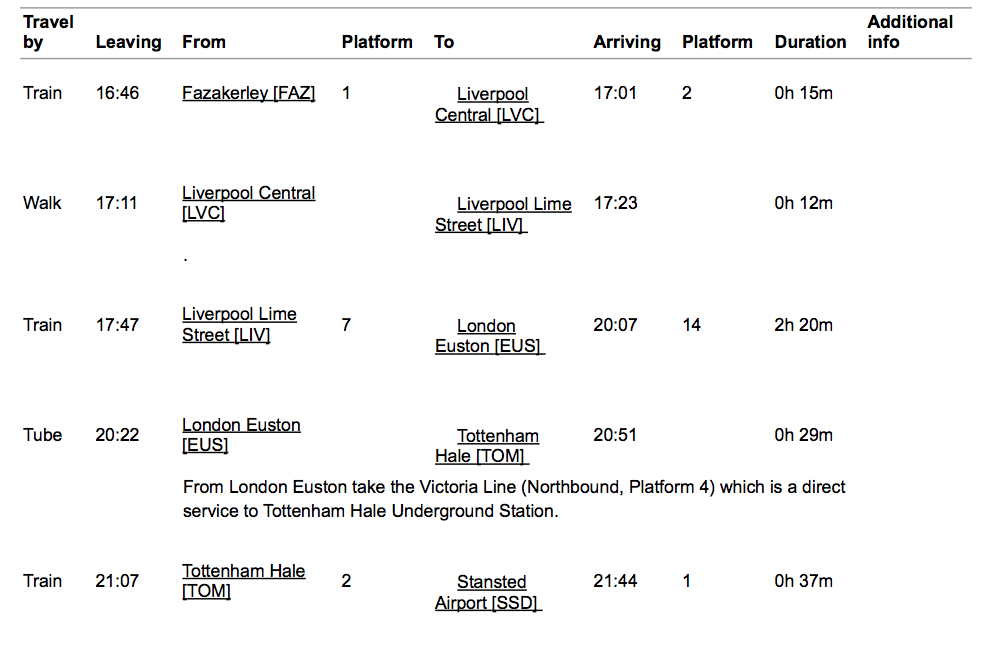
Unfortunately, I cannot find the EUS-TOM tube train at 20:22 with 29m journey.
I went to the National Rail site and I cannot find it - all the journeys are longer and have 1 change.
I understand that I will miss the earlier train which is 29m minutes and instead will have to take other train and make a change?
Any suggestions would be highly appreciated.

Unfortunately, I cannot find the EUS-TOM tube train at 20:22 with 29m journey.
I went to the National Rail site and I cannot find it - all the journeys are longer and have 1 change.
I understand that I will miss the earlier train which is 29m minutes and instead will have to take other train and make a change?
Any suggestions would be highly appreciated.
Last edited:

